독립 이표본 t-검정(Independent twosampletest)-두 그룹에서 추출된 표본이 서로 완전히 무관한 상태이므로 가정 쌍체 t-검정(Paired test)-두 그룹에서 관찰한 표본이 서로 짝을 이룬 상태
15.1 대응 표본에서 모평균 비교 대응 표본-대응 표본과 독립된 두 표본 사이의 차이 비교

15.1 대응 표본과 독립된 두 표본의 차이 비교
대응 표본에 대한 모 평균 차이(μd)
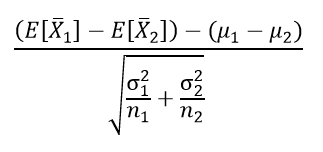
15.2 대응 표본에 대한 모 평균 차이(μd)~원래 쌍이 되지 않은 상태에서 쌍이 되지 않고 첫 번째 그룹에서 무작위로 n개를 추출, 두 번째는 서로 독립했을 때 생기는 문제는 만약 방해 요인(체중, 나이)이 자료 가격에 중대한 영향을 미친다면 즉 체중과 나이가 실제로 혈압을 상당히 많이 변동시키는 요인이라면 약의 차이로 인해 그룹을 만들어 놓았는데 이 안에 포함된 n인의 결과가 혈압이 울퉁불퉁해진다~평균에 관한 추론할 것으로 추측됩니다. 저
15.2 쌍체 t-검정 대응 표본에서 모평균 비교에 관한 쌍체 t-검정(pair dt-test)-가설 타입-관심 모수가 μd(그룹 간의 차이)로, 검정하고자 하는 모수의 경계치는 0이 되므로,
15.3 쌍처 t-검정 가설 유형-검정 계통과 표본 분포-대응 표본 간의 차이 d1, …, dn이 분산이 알려지지 않은 정규 분포를 따른다고 가정-검정 통계량 T는 귀무가설 H0:μd=0이 사실일 때,-유의 확률(p-value)의 계산-귀무가설 H0이 사실일 때, 검정 통계량 T의 분포 t0(=표본 자료에서 계산된 검정 통계량의 값)보다 대립 가설 방향에 따라 극단적인 값이 나올 확률
- 유의 수준(significance level) 100α%의 검정법-자료로부터 계산된 유의 확률(p-value)이 주어진 유의 수준α보다 작을 경우 귀무가설 H0을 기각 p-value γα 면, H0 기각
예제) 두 가지 진통제에 대한 상대적 효과 척도로 복용 후 숙면을 취할 수 있는 정도를 비교하고자 한다. 6명의 환자를 랜덤으로 추출해 각 환자에게 2가지 진통제를 각각 1회씩 복용 순서를 랜덤으로 정해 숙면 시간을 조사했다. 두 진통제 A, B로 인한 숙면 시간에 차이가 있다고나 할까. 유의수준 5%로 검정하시오. 단, 숙면시간 차이는 정규분포에 따른다.
15.4 쌍체 t-흑 예제
~ 같은 환자에 대해 두 번에 걸쳐 측정한 것은 쌍체검정용 자료를 만들기 위한 것!!! ***~숙면시간이 약 A, B에 따른 차이가 있는지 보고 싶은 것! 하지만 숙면시간은 개인별로 다르고 개인의 수면패턴을 반영하기 위해 같은 환자를 대상으로 2회에 걸쳐 실험한 것(어떤 사람은 수면시간이 길고 어떤 사람은 원래 수면시간이 짧을 수 있음)
- 가설 H0:μd=0H1:μd 00
- – 검정 통계량과 표본 분포 – 귀무가설 H0:μd=0이 사실일 때, – 검정 통계량의 관찰치 – 유의 확률 p-value는 P [T>2.98] ×2 = 0.0307
15.5 유의 확률 p-value-결론 P-value가 유의 수준 0.05보다 작으므로 귀무가설 기각→두 진통제에 의한 숙면 시간 차이는 있음